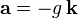Científicos:
http://prezi.com/mliv-1_n21xk/?utm_campaign=share&utm_medium=copy
martes, 29 de julio de 2014
Peso de un Cuerpo
Peso de un Cuerpo
El peso de un cuerpo es la fuerza que hay que oponerle a dicho cuerpo para que no caiga a la Tierra. El peso podemos sentirlo al sostener diferentes objetos a cierta altura.
Formulas:
m = w f = ma w = mg
g
Sistemas de Unidades de Peso:
La unidad gravitacional en el sistema Internacional es el Kgf y es el peso de 1 kg-masa.
1kgf = 9.8 Nt
1 Nt = 0.102 Kgf.
En el sistema CGS la unidad gravitacional es el gramo fuerza y el el peso de 1 gramo-masa.
En el sistema Ingles es la libra-fuerza que es el peso de 1 libra-masa.
1grf = 980 dinas
1 lbf = 32.2 Poundal
Equivalencia:
1 slug-m = 9.8 kg
1 slug = 32.2 lb.
Leyes de Newton
Isaac Newton (1642-1727)
Matemático, filosofo y físico Ingles, se hizo inmortal por el descubrimiento de las leyes de la gravitación universal, su explicación de la descomposición de la luz y sus notables trabajos de matemáticas. Formuló los fundamentos de la dinámica al enunciar las leyes que llevan su nombre: Le de Inercia, Ley de Fuerza y Ley de Acción y Reacción.Su libro mas importante se titula Principia Mathematica Philosophica donde establece los fundamentos de la mecánica.
Primera Ley de Newton (INERCIA):
Todo cuerpo en reposo tiende a seguir en reposo y todo cuerpo en movimiento tiende a seguir en movimiento rectilíneo uniforme, a menos que una fuerza externa no equilibrada actué sobre el.Segunda Ley de Newton (FUERZA):
Siempre que una fuerza no equilibrada actúa sobre un cuerpo produce una aceleración en la dirección y sentido de la fuerza que es directamente proporcional a la fuerza e inversamente proporcional a la mas del cuerpo.
Tercera Ley de Newton (ACCIÓN Y REACCIÓN):
Siempre que un cuerpo ejerce una fuerza (Acción) sobre otro, este reacciona con una fuerza (Reacción) de igual magnitud pero en sentido contrario.
Formulas:
a = f f = ma m = f
m a
"Unidades de medida de las Fuerzas"
En el sistema CGS la unidad de medida de fuerza es la dina que es la fuerza que actuando sobre un gramo-masa le logra imprimir una aceleración de 1cm/seg2.
En el sistema Internacional la unidad de fuerza es el Newton que es la fuerza que actuando sobre 1 kgm de masa le imprime una aceleración de 1mt/seg2.
En el sistema Ingles la unidad de fuerza es el Poundal que es la fuerza que actuando sobre 1 lb-mas le imprime una aceleración de 1 pie/seg2.
lunes, 23 de junio de 2014
Ejercicio de Potencia
Ejercicios de Potencia
1.- Un motor tiene una potencia de 40kw. Con que velocidad subirá un elevador cuyo peso es de 1500 kgf.
V= P F= 1500 kgf * 9.8 Nt = 14,700 Nt//
F 1 kgf
V= 40,000 w
14,700 Nt P= 40 kw * 1000 w = 40,000 w//
V= 2.72 mt/seg// 1 km
El ascensor de un edificio se mueve por medio de un motor cuya potencia es de 50 HP si tiene una masa de 1800 kg.Cuanto tiempo tardará en subir 40 mt.
T= F.S = 17640 Nt * 40mt t = T = 705,600 J t = 18.92 seg.//
T= 705600 J// P 37,300 J/Seg.
P= 50 HP * 746 W
1 HP
P= 37300 W//
En un tiempo de 3 minutos se sube un objeto que pesa 50 kgf a una altura de 15 mt. Qué trabajo se realizó y cual es la potencia.
T= F.S P= T P= 750 kgm P= 4.16 kgm/seg//
T= 50 kgf * 3 min t 180 seg.
T= 750 kgm//
POTENCIA
POTENCIA
Se le llama potencia a la rapidez con que se realiza un trabajo. La potencia es el cociente entre el trabajo y el tiempo empleado en realizar.
P= T
t
Unidades de Potencia: En el sistema CGS la unidad de potencia es el Ergio/Segundo (E/S) que es la potencia de un mecanismo que puede hacer un trabajo de un Ergio en un Segundo.
En el sistema Power (caballo de fuerza) (HP) el HP es la potencia de un mecanismo que puede efectuar un trabajo de 550librapie en 1 segundo. la LibraPie es el trabajo efectuado ppor una LibraFuerza al mover su punto de aplicación un pie en su propia dirección.
En el sistema Internacional la unidad de potencia es el Watt (W) que es la potencia de un mecanismo que puede hacer un trabajo de un Joul/Segundo.
1 kw = 1000 Watt 1 HP= 0.746 KW
1 libra-pie = 1.356 Joul 1 kw= 1.34 HP
1 HP = 746 Watt 1 HP= 76 kgm/seg.
Formula: P = F.V
Ejemplo: Calcular la potencia de un motor de un carro en HP que desarrolla una fuerza de atracción de 110 kgf cuando su velocidad es de 90 km/h.
90km/h = 25 mt/seg
P=F.V
P= 110kgf *25mt/seg
P= 2,750 kgm/seg//
P= 2,750 kgm/seg = 1 HP = 36.18 HP//
76 kgm/seg.
En el sistema Power (caballo de fuerza) (HP) el HP es la potencia de un mecanismo que puede efectuar un trabajo de 550librapie en 1 segundo. la LibraPie es el trabajo efectuado ppor una LibraFuerza al mover su punto de aplicación un pie en su propia dirección.
En el sistema Internacional la unidad de potencia es el Watt (W) que es la potencia de un mecanismo que puede hacer un trabajo de un Joul/Segundo.
1 kw = 1000 Watt 1 HP= 0.746 KW
1 libra-pie = 1.356 Joul 1 kw= 1.34 HP
1 HP = 746 Watt 1 HP= 76 kgm/seg.
Formula: P = F.V
Ejemplo: Calcular la potencia de un motor de un carro en HP que desarrolla una fuerza de atracción de 110 kgf cuando su velocidad es de 90 km/h.
90km/h = 25 mt/seg
P=F.V
P= 110kgf *25mt/seg
P= 2,750 kgm/seg//
P= 2,750 kgm/seg = 1 HP = 36.18 HP//
76 kgm/seg.
EJERCICIOS
EJERCICIOS.
Calcule la distancia recorrida por el punto de aplicación de una fuerza de 4.5 Nt si el trabajo es de 13.5 Joules.
S= T
F
S= 13.5 Nt * mt
4.5 Nt
S= 3 mt//
Que trabajo hace una fuerza de 110 Nt cuando mueve su punto de aplicación de 20 mt en su misma dirección?
T= F*S
T= 110 Nt * 20 mt
T= 2,200 Joules//
Calcule la distancia recorrida por el punto de aplicación de una fuerza de 4.5 Nt si el trabajo es de 13.5 Joules.
S= T
F
S= 13.5 Nt * mt
4.5 Nt
S= 3 mt//
Que trabajo hace una fuerza de 110 Nt cuando mueve su punto de aplicación de 20 mt en su misma dirección?
T= F*S
T= 110 Nt * 20 mt
T= 2,200 Joules//
ejercicios
Ejercicios:
Un cuerpo cuya masa es de 120 kg se levanta hasta una altura de 15mt halando con una cuerda a lo largo de un plano inclinado que tiene una inclinación de 30°. Sabiendo que la fuerza ejercida en la cuerda es de 900 Nt y el coeficiente de rozamiento es de 0.25. Encuentre: a) el trabajo realizado por cada fuerza. b) el trabajo total realizado al subir el cuerpo.
S= 15mt = 30 mt
Sen30°
Tf= F*S Wx= mg.sen o(
Tf= 900 Nt * 30mt Wx= 120kg(9.8mt/seg) Sen 30°
Tf= 27,000 Joules// Wx= 58 Nt//
N= mg cos Ө Tw= - Wx * S
N= 120kg (9.8) Cos 30° Tw= -58 Nt * 30mt
N= 1,018.44 Nt// Tw= -17,640 Joules//
TN= N*S Cos Ө Fr= U N
TN= 1018.44 Nt * 30mt Cos 90° Fr= 0.25 * 1,018.44
TN= 0// Fr= - 254.61//
Tr= -FR * S Tt= Tf + Tn + Tw + Tr
Tr= -(-254.61) * 30mt Tt= 27,000 + 0 + (-17,640) + (-7683.3)
Tr= -7638.3// Tt= 1676.7//
Calcule el trabajo efectuado por una fuerza de 85 Nt cuyo punto de aplicación se desplaza 53 mt en la dirección de la fuerza. Dar la respuesta en Kgm, Joules y ERG.
T= F*S
T= 85 Nt * 53 mt
T= 4,505 Joules//
T= 4,505 J * 1 kgm = 459.69 Kgm//
9.8 Nt
T= 4,505 J * 107 = 4.505X1010ERG//
Un cuerpo cuya masa es de 120 kg se levanta hasta una altura de 15mt halando con una cuerda a lo largo de un plano inclinado que tiene una inclinación de 30°. Sabiendo que la fuerza ejercida en la cuerda es de 900 Nt y el coeficiente de rozamiento es de 0.25. Encuentre: a) el trabajo realizado por cada fuerza. b) el trabajo total realizado al subir el cuerpo.
S= 15mt = 30 mt
Sen30°
Tf= F*S Wx= mg.sen o(
Tf= 900 Nt * 30mt Wx= 120kg(9.8mt/seg) Sen 30°
Tf= 27,000 Joules// Wx= 58 Nt//
N= mg cos Ө Tw= - Wx * S
N= 120kg (9.8) Cos 30° Tw= -58 Nt * 30mt
N= 1,018.44 Nt// Tw= -17,640 Joules//
TN= N*S Cos Ө Fr= U N
TN= 1018.44 Nt * 30mt Cos 90° Fr= 0.25 * 1,018.44
TN= 0// Fr= - 254.61//
Tr= -FR * S Tt= Tf + Tn + Tw + Tr
Tr= -(-254.61) * 30mt Tt= 27,000 + 0 + (-17,640) + (-7683.3)
Tr= -7638.3// Tt= 1676.7//
Calcule el trabajo efectuado por una fuerza de 85 Nt cuyo punto de aplicación se desplaza 53 mt en la dirección de la fuerza. Dar la respuesta en Kgm, Joules y ERG.
T= F*S
T= 85 Nt * 53 mt
T= 4,505 Joules//
T= 4,505 J * 1 kgm = 459.69 Kgm//
9.8 Nt
T= 4,505 J * 107 = 4.505X1010ERG//
Ejercicios
EJERCICIOS DE TRABAJO
1.-Calcular en JOules, Kgm y Ergios el trabajo de una fuerza de 3,000 Nt cuyo punto de aplicación se desplaza 80 mt en dirección de la fuerza.
T= F.S
T= 3,000 Nt * 80 mt
T= 240,000 Joules//
T=240,000 J * 1kgm = 24,49.79 Kgm//
9.8 Nt
T= 240,000 J * 107 = 2.4 X 1012 Ergios//
2.- Calcular la distancia recorrida por el punto de aplicación de una fuerza de 90 Nt, si el trabajo efectuado es de 450 Joules.
S= T
F
S= 450
90
S= 5 //
3.- Un carrito se desplaza 25 mt por acción de una fuerza de 15 Nt a través del cordel que forma una angulo de 60° con la horizontal, calcular el trabajo realizado.
T= F.S Cos Ө
T= 15 Nt * 25 mt Cos 60°
T= 187.5 //
Trabajo
TRABAJO:
Para hallar trabajo se utilizan las siguientes formulas:
T= F.S
T= F.S Cos Ө
UNIDADES DE TRABAJO:
a) Joules a Ergios
1 J = 107 Dinas
b) Kilogramos a Joules
1 kgm = 9.8 Nt
Ejemplo:
Calcular el trabajo efectuado por una fuerza de 225 dinas al mover su punto de aplicación 5mt en su propia dirección.
T= F.S 5mt= 500 cm//
T= 225 dinas * 500 cm
T= 112,500 Ergios//
jueves, 6 de marzo de 2014
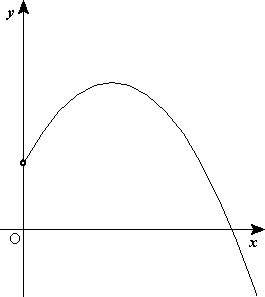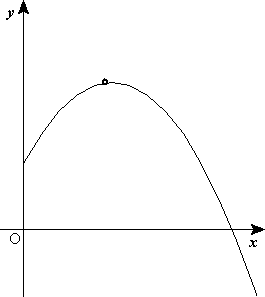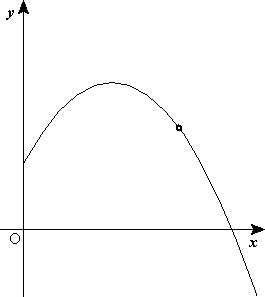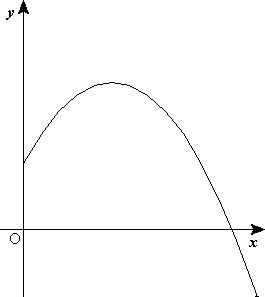
TIRO PARABOLICO
TIRO PARABÓLICO
Se denomina movimiento parabólico al realizado por un objeto cuya trayectoria describe una parábola. Se corresponde con la trayectoria ideal de un proyectil que se mueve en un medio que no ofrece resistencia al avance y que está sujeto a un campo gravitatorio uniforme.
Puede ser analizado como la composición de dos movimientos rectilíneos: un movimiento rectilíneo uniforme horizontal y un movimiento rectilíneo uniformemente acelerado vertical.
Movimiento parabólico (completo)
El movimiento parabólico completo se puede considerar como la composición de un avance horizontal rectilíneo uniforme y un lanzamiento vertical hacia arriba, que es un movimiento rectilíneo uniformemente acelerado hacia abajo (MRUV) por la acción de la gravedad.
En condiciones ideales de resistencia al avance nulo y campo gravitatorio uniforme, lo anterior implica que:
- Un cuerpo que se deja caer libremente y otro que es lanzado horizontalmente desde la misma altura tardan lo mismo en llegar al suelo.
- La independencia de la masa en la caída libre y el lanzamiento vertical es igual de válida en los movimientos parabólicos.
- Un cuerpo lanzado verticalmente hacia arriba y otro parabólica mente completo que alcance la misma altura tarda lo mismo en caer.
Ecuaciones del movimiento parabólico
Hay dos ecuaciones que rigen el movimiento parabólico:donde: es el módulo de la velocidad inicial.
es el módulo de la velocidad inicial. es el ángulo de la velocidad inicial sobre la horizontal.
es el ángulo de la velocidad inicial sobre la horizontal. es la aceleración de la gravedad.
es la aceleración de la gravedad. son dos versores (vectores unitarios) en el plano.
son dos versores (vectores unitarios) en el plano.
La velocidad inicial se compone de dos partes: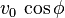 que se denomina componente horizontal de la velocidad inicial.
que se denomina componente horizontal de la velocidad inicial.
- En lo sucesivo

- En lo sucesivo
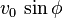 que se denomina componente vertical de la velocidad inicial.
que se denomina componente vertical de la velocidad inicial.
- En lo sucesivo
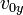
- En lo sucesivo
Se puede expresar la velocidad inicial de este modo: : [ecu. 1]
: [ecu. 1]
Será la que se utilice, excepto en los casos en los que deba tenerse en cuenta el ángulo de la velocidad inicial.Ecuación de la aceleración
La única aceleración que interviene en este movimiento es la constante de la gravedad, que corresponde a la ecuación:que es vertical y hacia abajo.Ecuación de la velocidad
La velocidad de un cuerpo que sigue una trayectoria parabólica se puede obtener integrando la siguiente ecuación: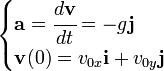 La integración es muy sencilla por tratarse de una ecuación diferencial de primer orden y el resultado final es:
La integración es muy sencilla por tratarse de una ecuación diferencial de primer orden y el resultado final es:
Ecuación de la posición
Partiendo de la ecuación que establece la velocidad del móvil con la relación al tiempo y de la definición de velocidad, la posición puede ser encontrada integrando de la siguiente ecuación diferencial: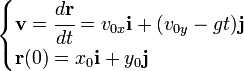 La integración es muy sencilla por tratarse de una ecuación diferencial de primer ordeny el resultado final es:
La integración es muy sencilla por tratarse de una ecuación diferencial de primer ordeny el resultado final es:
martes, 18 de febrero de 2014
CAIDA LIBRE
"CAIDA LIBRE"
En física, se denomina caída libre al movimiento de un cuerpo bajo la acción exclusiva de un campo gravitatorio. Esta definición formal excluye a todas las caídas reales influenciadas en mayor o menor medida por la resistencia aerodinámica del aire, así como a cualquier otra que tenga lugar en el seno de un fluido; sin embargo es frecuente también referirse coloquial mente a éstas como caídas libres, aunque los efectos de la viscosidad del medio no sean por lo general despreciables.
El concepto es aplicable también a objetos en movimiento vertical ascendente sometidos a la acción desaceleradora de la gravedad, como un disparo vertical; o a satélites en órbita alrededor de la Tierra o de cualquier otro cuerpo celeste. Otros sucesos referidos también como caída libre lo constituyen las trayectorias geodésicas en el espacio-tiempo descritas en la teoría de la relatividad general.
Ejemplos de caída libre deportiva los encontramos en actividades basadas en dejarse caer una persona a través de la atmósfera sin sustentación alar ni de paracaídas durante un cierto trayecto.
El movimiento del cuerpo en caída libre es vertical con velocidad creciente (aproximadamente movimiento uniformemente acelerado con aceleración g) (aproximadamente porque la velocidad aumenta cuando el objeto disminuye en altura, en la mayoría de los casos la variación es despreciable). La ecuación de movimiento se puede escribir en términos la altura y:
(1)
donde:
 , son la aceleración y la velocidad verticales.
, son la aceleración y la velocidad verticales. , es la fuerza de rozamiento fluido dinámico (que aumenta con la velocidad).
, es la fuerza de rozamiento fluido dinámico (que aumenta con la velocidad).
- Si, en primera aproximación, se desprecia la fuerza de rozamiento, cosa que puede hacerse para caídas desde pequeñas alturas de cuerpos relativamente compactos, en las que se alcanzan velocidades moderadas, la solución de la ecuación diferencial (1) para las velocidades y la altura vienen dada por:
donde v0 es la velocidad inicial, para una caída desde el reposo v0 = 0 y h0 es la altura inicial de caída.
- Para grandes alturas u objetos de gran superficie (una pluma, un paracaídas) es necesario tener en cuenta la resistencia fluidodinámica que suele ser modelizada como una fuerza proporcional a la velocidad, siendo la constante de proporcionalidad el llamado rozamiento aerodinámico kw:
(2)
En este caso la variación con el tiempo de la velocidad y el espacio recorrido vienen dados por la solución de la ecuación diferencial (2):
Nótese que en este caso existe una velocidad límite dada por el rozamiento aerodinámico y la masa del cuerpo que cae:
lunes, 17 de febrero de 2014
GALILEO GALILEI
GALILEO GALILEI
Galileo Galilei (Pisa, 15 de febrero de 1564 – Arcetri, 8 de enero de 1642) fue un astrónomo, filósofo, matemático y físico italiano que estuvo relacionado estrechamente con la revolución científica. Eminente hombre del Renacimiento, mostró interés por casi todas las ciencias y artes (música, literatura, pintura). Sus logros incluyen la mejora deltelescopio, gran variedad de observaciones astronómicas, la primera ley del movimiento y un apoyo determinante para el copernicanismo. Ha sido considerado como el «padre de la astronomía moderna», el «padre de la física moderna y el padre de la ciencia.
Su trabajo experimental es considerado complementario a los escritos de Francis Bacon en el establecimiento del moderno método científico y su carrera científica es complementaria a la de Johannes Kepler. Su trabajo se considera una ruptura de las teorías asentadas de la física aristotélica y su enfrentamiento con la Inquisición romana de la Iglesia católica suele presentarse como el mejor ejemplo de conflicto entre religióny ciencia en la sociedad occidental.
Galileo, que nació en Pisa cuando ésta pertenecía al Gran Ducado de Toscana, fue el mayor de seis hermanos y fue hijo de un músicoy matemático florentino llamado Vincenzo Galilei, que quería que su hijo mayor estudiase medicina. Los Galilei, que eran una familia de la baja nobleza y se ganaban la vida gracias al comercio, se encargaron de la educación de Galileo hasta los 10 años, edad a la que pasó a cargo de un vecino religioso llamado Jacobo Borhini cuando sus padres se trasladaron a Florencia. Por mediación de este, el pequeño Galileo accedió al convento de Santa María de Vallombrosa (Florencia) y recibió una formación más religiosa que le llevó a plantearse unirse a la vida religiosa, algo que a su padre le disgustó. Por eso, Vincenzo Galileo —un señor bastante escéptico— aprovechó una infección en el ojo que padecía su hijo para sacarle del convento alegando «falta de cuidados. Dos años más tarde, Galileo fue inscrito por su padre en la Universidad de Pisa, donde estudió medicina, filosofía y matemáticas.
En 1583 Galileo se inicia en la matemática por medio de Ostilio Ricci, un amigo de la familia, alumno de Tartaglia. Ricci tenía la costumbre, rara en esa época, de unir la teoría a la práctica experimental.
Atraído por la obra de Euclides, sin ningún interés por la medicina y todavía menos por las disputas escolásticas y la filosofía aristotélica, Galileo reorienta sus estudios hacia las matemáticas. Desde entonces, se siente seguidor de Pitágoras, de Platón y deArquímedes y opuesto al aristotelismo. Todavía estudiante, descubre la ley de la isocronía de los péndulos, primera etapa de lo que será el descubrimiento de una nueva ciencia: la mecánica. Dentro de la corriente humanista, redacta también un panfleto feroz contra el profesorado de su tiempo. Toda su vida, Galileo rechazará el ser comparado a los profesores de su época, lo que le supondrá numerosos enemigos.
Dos años más tarde, retorna a Florencia sin diploma, pero con grandes conocimientos y una gran curiosidad científica.
MRUV
Movimiento rectilíneo uniformemente variado (MRUV)
En este tipo de movimiento a diferencia del MRU (movimiento rectilíneo uniforme), la velocidadvaría. Pero esta variación a su vez es con un cierto orden, es decir que cambia un mismo intervalo en una misma cantidad de tiempo.
Por este hecho aparece una nueva magnitud llamada aceleración. La aceleración está representada por la fórmula:
a = (Vf – Vi) / T
La a es la aceleración, Vi es la velocidad del inicio y Vf es la velocidad final.
Para calcular la distancia recorrida se usa la siguiente fórmula:
D = Vi . T +/- ½ . a . T2
El signo positivo del segundo miembro se usa cuando el movimiento experimenta un aumento en su velocidad. Es una aceleración positiva. El signo menos se usa en situaciones de descenso de la velocidad, o sea una aceleración negativa. Aquí vemos otra diferencia con respecto al MRU en el cual la distancia se calcula de forma mucho más sencilla.
PROBLEMAS:
Calcula la distancia recorrida por un móvil que parte de reposo y alcanza una velocidad de 52 Km/h en 5 segundos.
Usaremos la formula:
D = Vi . T +/- ½ . a . T2
Tenemos como datos la velocidad final y el tiempo. Como el móvil parte del reposo su velocidad inicial es 0, por lo tanto el primer termino se anula.
D = + ½ . a . T2
El signo de la aceleración queda positivo ya que la velocidad aumenta de 0 al valor final de 52 Km/h.
La aceleración no la tenemos pero la podemos calcular. Para esto será conveniente previamente pasar la unidad de velocidad de Km/h a mts/seg para que sea compatible con el tiempo que esté expresado en segundos.
Ahora procedemos a calcular la aceleración:
D = + ½ . 2,89 mts/seg2 . (5 seg)2
D = 36.125 mts.
Calcula la velocidad final de un móvil que viajando a una velocidad de 22 mts/seg acelera a razón de 2 mts/seg2 en 4 seg.
De la formula de aceleración hay que despejar la velocidad final.
a = (Vf – Vi) / T
Vf = a x T + Vi
Vf = 2 mts/seg2 x 4 seg + 22 mts/seg
Vf = 30 mts/seg
MRU
"MRU"
Un movimiento es rectilíneo cuando un móvil describe una trayectoria recta, y es uniforme cuando su velocidad es constante en el tiempo, dado que su aceleración es nula. Nos referimos a él mediante el MRU.
- Movimiento que se realiza sobre una línea recta.
- Velocidad constante; implica magnitud y dirección constantes.
- La magnitud de la velocidad recibe el nombre de celeridad o rapidez.
- Aceleración nula.
Ejemplo: Calcula la posición final de un móvil que parte a 10 metros del origen con una velocidad igual a 45 Km/h durante 5 segundos.
En el apartado de pasaje de unidades describimos como se hacen los pasajes de velocidad de una unidad a otra. 45 Km/h equivalen a 12.5 mts/seg. Entonces:
X = 10 mts + 12.5 mts/seg. 5seg
X = 72.5 mts.
Volviendo a la primera fórmula veremos algunos ejemplos prácticos
Calcula la velocidad de un móvil que recorre 230 kms en 1.8 hs
V = D / t
V = 230 kms / 1.8 hs
V = 127.78 Kms/h
Calcula la distancia que recorre un atleta que corre a una velocidad de 9 mts/seg durante 16 segundos.
Despejamos la distancia de la fórmula V = d / t
D = V x t
D = 9 mts / seg x 16 seg
D = 144 mts.
En cuanto tiempo un vehículo recorrerá un tramo de 68 km si marcha a una velocidad de 82 Km/h.
T = D / V
T = 68 km / 82 Km/h
T = 0.83 hs.
Como no es un número muy adecuado para expresar la hora la pasamos a minutos
0,83 hs = 49 min y 45 seg (Ver pasaje de unidades)
Para finalizar veremos los gráficos que describen a este movimiento.
Distancia versus tiempo. La gráfica es una recta.
Velocidad versus tiempo. En este caso como la velocidad no varía, se representa con una línea paralela y recta. No tiene pendiente porque no varía.
Suscribirse a:
Comentarios (Atom)